Descente polarisation de concentration
Analyse de la polarisation de concentration
La filtration d'une solution de PVP a été réalisée sur une membrane plane (voir video). L'opérateur réalise des expériences en mettant dans le réservoir une solution de PVP (90 kDa) concentrée (fiche CAS et exemple d'utilisation en agroalimentaire). La masse molaire de la PVP est bien plus grande que le seuil de coupure de la membrane (15kDa) : la PVP est donc totalement retenu par la membrane et la concentration en PVP dans le perméat est nulle.
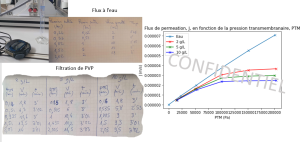
L'opérateur a noté les valeurs mesurées sur les papiers ci-contre. Un stagiaire de licence a ensuite consigné l'ensemble des mesures dans des tableaux Python (voir code ci-dessous) et il a tracé les courbes ci-contre.
Code Python avec les valeurs mesurées à l'eau (pour le calcul de la perméabilité)
1
import numpy as np
2
import matplotlib.pyplot as plt
3
4
#Valeurs de pression transmembranaire5
PTM_bar_alim=np.array([0,0.24,0.53,1.02,1.52,2.02])
6
PTM_bar_ret=np.array([0,0.22,0.51,1.,1.5,2.0])
7
PTM = 1e5*(PTM_bar_alim + PTM_bar_ret)/2 #calcul de la PTM en Pa
8
9
#Valeurs de volume filtré en ml 10
V=np.array([0,2,5,10,14,18])
11
#Valeurs de temps en s correspondant aux volumes 12
t=np.array([1,105,120,125,120,120])
13
14
#Equations permettant de calculer le débit de permeation, Q, puis le flux de permeation, J15
Q=V*1e-6/t #m3/s
16
S=106.*2. #cm2
17
J=Q/(S*1e-4) #m/s
18
19
'''#Vérifier les valeurs 20
print('Pression transmembranaire en Pa')21
print(PTM)22
print('Flux de permation en m/s')23
print(J)'''24
25
plt.plot(PTM, J, marker='x')
26
plt.title('Flux de permeation, J, en fonction de la pression transmembranaire, PTM')
27
plt.xlabel('PTM (Pa)')
28
plt.ylabel('J (m/s)')
29
30
#regression lineaire pour la determination de la resistance hydraulique31
reglin_perm= np.polyfit(PTM,J,1)
32
pente_perm=reglin_perm[0]
33
oo_perm=reglin_perm[1]
34
plt.plot(PTM, pente_perm*PTM+oo_perm, 'g--')
35
36
#calcul de la résistance hydraulique37
mu=0.001 #Pa.s ou kg m-1 s-1
38
Rm=1/(mu*pente_perm)
39
print('Permeabilité de la membrane, Lp=', pente_perm*1000*3600*1e5,' L/(h.m2.bar)')
40
print('Resistance hydraulique de la membrane, Rm=', Rm,'m-1')
import numpy as np
import matplotlib.pyplot as plt
#Valeurs de pression transmembranaire
PTM_bar_alim=np.array([0,0.24,0.53,1.02,1.52,2.02])
PTM_bar_ret=np.array([0,0.22,0.51,1.,1.5,2.0])
PTM = 1e5*(PTM_bar_alim + PTM_bar_ret)/2 #calcul de la PTM en Pa
#Valeurs de volume filtré en ml
V=np.array([0,2,5,10,14,18])
#Valeurs de temps en s correspondant aux volumes
t=np.array([1,105,120,125,120,120])
#Equations permettant de calculer le débit de permeation, Q, puis le flux de permeation, J
Q=V*1e-6/t #m3/s
S=106.*2. #cm2
J=Q/(S*1e-4) #m/s
'''#Vérifier les valeurs
print('Pression transmembranaire en Pa')
print(PTM)
print('Flux de permation en m/s')
print(J)'''
plt.plot(PTM, J, marker='x')
plt.title('Flux de permeation, J, en fonction de la pression transmembranaire, PTM')
plt.xlabel('PTM (Pa)')
plt.ylabel('J (m/s)')
#regression lineaire pour la determination de la resistance hydraulique
reglin_perm= np.polyfit(PTM,J,1)
pente_perm=reglin_perm[0]
oo_perm=reglin_perm[1]
plt.plot(PTM, pente_perm*PTM+oo_perm, 'g--')
#calcul de la résistance hydraulique
mu=0.001 #Pa.s ou kg m-1 s-1
Rm=1/(mu*pente_perm)
print('Permeabilité de la membrane, Lp=', pente_perm*1000*3600*1e5,' L/(h.m2.bar)')
print('Resistance hydraulique de la membrane, Rm=', Rm,'m-1')Code Python avec les valeurs mesurées lors de filtration de PVP
1
#Tableaux de PTM2
PTM_bar_2gl=np.array([0.14,0.51,0.995,1.51,2.03])
3
PTM_bar_5gl=np.array([0.15,0.505,1,1.495,2.005])
4
PTM_bar_10gl=np.array([0.16,0.535,1.005,1.5,2.03])
5
#Tableaux de volume en ml 6
V_2gl=np.array([1.8,6.3,11.6,13.5,14])
7
V_5gl=np.array([1.8,6.,10.4,11.2,11.5])
8
V_10gl=np.array([1.8,5.8,9,9.3,9.5])
9
#Tableau de temps en s correspondant 10
t_2gl=np.array([180,182,180,181,181])
11
t_5gl=np.array([180,180,181,182,183])
12
t_10gl=np.array([180,179,180,181,182])
13
14
#Calcul des PTM en Pa15
PTM_2gl=1e5*PTM_bar_2gl
16
PTM_5gl=1e5*PTM_bar_5gl
17
PTM_10gl=1e5*PTM_bar_10gl
18
19
#Calculs des flux de perméation20
J_2gl=(V_2gl*1e-6/t_2gl)/(S*1e-4) #m/s
21
J_5gl=(V_5gl*1e-6/t_5gl)/(S*1e-4) #m/s
22
J_10gl=(V_10gl*1e-6/t_10gl)/(S*1e-4) #m/s
23
'''print('J 2gl',J_2gl)24
print('J 5gl',J_5gl)25
print('J 10gl',J_10gl)'''26
27
#Tracé des flux de permeation28
plt.plot(PTM, J, marker='x', label='Eau')
29
plt.plot(PTM_2gl, J_2gl, marker='x', color='r', label='2 g/L')
30
plt.plot(PTM_5gl, J_5gl, marker='x', color='g', label='5 g/L')
31
plt.plot(PTM_10gl, J_10gl, marker='x', color='b', label='10 g/L')
32
plt.legend(loc='best')
33
plt.title('Flux de permeation, J, en fonction de la pression transmembranaire, PTM')
34
plt.xlabel('PTM (Pa)')
35
plt.ylabel('J (m/s)')
36
plt.show()
#Tableaux de PTM
PTM_bar_2gl=np.array([0.14,0.51,0.995,1.51,2.03])
PTM_bar_5gl=np.array([0.15,0.505,1,1.495,2.005])
PTM_bar_10gl=np.array([0.16,0.535,1.005,1.5,2.03])
#Tableaux de volume en ml
V_2gl=np.array([1.8,6.3,11.6,13.5,14])
V_5gl=np.array([1.8,6.,10.4,11.2,11.5])
V_10gl=np.array([1.8,5.8,9,9.3,9.5])
#Tableau de temps en s correspondant
t_2gl=np.array([180,182,180,181,181])
t_5gl=np.array([180,180,181,182,183])
t_10gl=np.array([180,179,180,181,182])
#Calcul des PTM en Pa
PTM_2gl=1e5*PTM_bar_2gl
PTM_5gl=1e5*PTM_bar_5gl
PTM_10gl=1e5*PTM_bar_10gl
#Calculs des flux de perméation
J_2gl=(V_2gl*1e-6/t_2gl)/(S*1e-4) #m/s
J_5gl=(V_5gl*1e-6/t_5gl)/(S*1e-4) #m/s
J_10gl=(V_10gl*1e-6/t_10gl)/(S*1e-4) #m/s
'''print('J 2gl',J_2gl)
print('J 5gl',J_5gl)
print('J 10gl',J_10gl)'''
#Tracé des flux de permeation
plt.plot(PTM, J, marker='x', label='Eau')
plt.plot(PTM_2gl, J_2gl, marker='x', color='r', label='2 g/L')
plt.plot(PTM_5gl, J_5gl, marker='x', color='g', label='5 g/L')
plt.plot(PTM_10gl, J_10gl, marker='x', color='b', label='10 g/L')
plt.legend(loc='best')
plt.title('Flux de permeation, J, en fonction de la pression transmembranaire, PTM')
plt.xlabel('PTM (Pa)')
plt.ylabel('J (m/s)')
plt.show()Donner la contre pression osmotique correspondant à la solution de 10 g/L filtrée à une pression de 1,5 bar. Le bout de code suivant devrait vous aider (1,5 bar est la quatrième mesure et vous devez utiliser donc l'index 3 pour la récupérer dans le tableau Python puisque la numérotation dans les tableaux commence à 0 [0, 1, 2 , 3 ...])
1
Pi_cm_10gl=PTM_10gl-(J_10gl*mu*Rm)
2
print ('Contre pression osmotique à 1,5 bar : ', Pi_cm_10gl[3]/1e5, ' bar')
Pi_cm_10gl=PTM_10gl-(J_10gl*mu*Rm)
print ('Contre pression osmotique à 1,5 bar : ', Pi_cm_10gl[3]/1e5, ' bar')Analyse de la polarisation de concentration
En déduire la concentration à la membrane en g/L ?
(vous aurez besoin de suivre le tuto Python "résolution d'une équation à 1 inconnu" au Bar "Jus de fruit pour avoir la pression osmotique")
1
#Fonction devant être égale à zero pour trouver la concentration en PVP, c (en g/L)2
#correspondant à une pression osmotique, pi (en Pa)3
def pic(c,pi):
4
c=c/1000. #concentration en g/cm3
5
pic=0.210*c+16.05*c*c+163.8*c**3 #Pression osmotique en bar
6
return pic*1e5-pi #écart entre calcul et valeur souhaitée
7
8
cm=fsolve(pic,2, args=Pi_cm_10gl[3])
9
print ('La concentration à la membrane est :',cm , ' g/L')
#Fonction devant être égale à zero pour trouver la concentration en PVP, c (en g/L)
#correspondant à une pression osmotique, pi (en Pa)
def pic(c,pi):
c=c/1000. #concentration en g/cm3
pic=0.210*c+16.05*c*c+163.8*c**3 #Pression osmotique en bar
return pic*1e5-pi #écart entre calcul et valeur souhaitée
cm=fsolve(pic,2, args=Pi_cm_10gl[3])
print ('La concentration à la membrane est :',cm , ' g/L')Analyse de la polarisation de concentration
Utilisez cette dernière valeur pour estimer le coefficient de transfert de matière en m/s à l'aide de la loi du film.
1
k_10gl=J_10gl[3]/((np.log(cm))-(np.log(10)))
k_10gl=J_10gl[3]/((np.log(cm))-(np.log(10)))
Analyse de la polarisation de concentration
Utilisez le modèle du gel pour estimer le coefficient de transfert de matière et la concentration de gel. Donnez la concentration de gel obtenue.
1
#Tableaux des valeurs de concentration, C02
c0=np.array([2,5,10]) #g/L
3
lnc0=np.log(c0)
4
5
#Tableaux des valeurs de flux limite (l'indice -1 permet de trouver la dernière valeur d'un tableau)6
Jlim=np.array([J_2gl[-1],J_5gl[-1],J_10gl[-1]]) #m/s
7
8
#regression lineaire9
reg= np.polyfit(lnc0,Jlim,1)
10
pente_k=reg[0]
11
oo_klncg=reg[1]
12
plt.plot(lnc0, Jlim, 'x')
13
plt.plot(lnc0, pente_k*lnc0+oo_klncg, 'r--')
14
plt.title('Flux limite, Jlim, en fonction du log de la concentration')
15
plt.xlabel('ln(c0) (-)')
16
plt.ylabel('Jlim (m/s)')
17
18
#INSERER L'EQUATION POUR CALCULER LA CONCENTRATION DE GEL19
print('Coefficient de transfert de matière, k=',-pente_k, 'm/s')
20
cg= SNOW NEIGE SNOW NEIGE ZUT
21
print('La concentration de gel est de ', cg, 'g/L')
#Tableaux des valeurs de concentration, C0
c0=np.array([2,5,10]) #g/L
lnc0=np.log(c0)
#Tableaux des valeurs de flux limite (l'indice -1 permet de trouver la dernière valeur d'un tableau)
Jlim=np.array([J_2gl[-1],J_5gl[-1],J_10gl[-1]]) #m/s
#regression lineaire
reg= np.polyfit(lnc0,Jlim,1)
pente_k=reg[0]
oo_klncg=reg[1]
plt.plot(lnc0, Jlim, 'x')
plt.plot(lnc0, pente_k*lnc0+oo_klncg, 'r--')
plt.title('Flux limite, Jlim, en fonction du log de la concentration')
plt.xlabel('ln(c0) (-)')
plt.ylabel('Jlim (m/s)')
#INSERER L'EQUATION POUR CALCULER LA CONCENTRATION DE GEL
print('Coefficient de transfert de matière, k=',-pente_k, 'm/s')
cg= SNOW NEIGE SNOW NEIGE ZUT
print('La concentration de gel est de ', cg, 'g/L')Vous avez tenté plus de 100 fois cet exercice, veuillez poursuivre le parcours.