Rétention
Lors d'une filtration d'une dispersion à une concentration, \(c_0\), la transmission des espèces à travers la membrane dépend de la concentration en espèce à la membrane, \(c_m\). L'augmentation de la concentration à la membrane engendre une augmentation de la concentration dans le perméat, \(c_p\).
Ces différentes concentrations peuvent amener à définir différemment les rétentions ou les transmissions. Expérimentalement, lorsqu'on réalise une filtration, on connaît la concentration dans la dispersion à filtrer, \(c_0\), et on peut mesurer la concentration dans le perméat, \(c_p\)
On définit alors une transmission, \(Tr_{obs}\), et une rétention, \(R_{obs}\) observées (le terme observé caractérise le fait qu'elle soit mesurée expérimentalement) :
\(Tr_{obs}=\frac{c_p}{c_0}\)
\(R_{obs}=1-\frac{c_p}{c_0}\)
A noter que la transmission est de 0 % et la rétention de 100 % quand la membrane retient totalement une espèce.
On peut également définir ces paramètres en considérant la concentration à la membrane et la concentration dans le perméat qui sont les concentrations aux bornes de la membrane. On utilise alors le terme intrinsèque car ces propriétés sont intrinsèques aux propriétés de la membrane (taille de pore, charge ...).
\(Tr_{int}=\frac{c_p}{c_m}\)
\(R_{int}=1-\frac{c_p}{c_m}\)
La loi du film que nous avons vu précédemment permet de relier les différentes concentrations au paramètre de filtration via le nombre de Péclet :
\(\frac{c_m-c_p}{c_0-c_p}=e^{Pe}\)
On peut alors combiner les équations précédentes pour relier la rétention observée à la rétention intrinsèque et au nombre de Péclet. Après quelques lignes de manipulation mathématique :
\(\frac{\frac{c_m}{c_p}-1}{\frac{c_0}{c_p}-1}=e^{Pe}\)
\(\frac{\frac{1}{1-R_{int}}-1}{\frac{1}{1-R_{obs}}-1}=e^{Pe}\)
\(\frac{1}{1-R_{obs}}-1=(\frac{1}{1-R_{int}}-1)e^{-Pe}\)
On obtient la relation suivante :
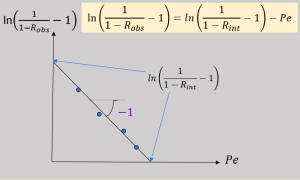
\(ln(\frac{1}{1-R_{obs}}-1)=ln(\frac{1}{1-R_{int}}-1)-Pe\)
On peut utiliser ce modèle en déterminant des retentions expérimentales en fonction de différents nombres de Péclet (c'est à dire pour différents flux de perméation ou différentes vitesses de balayage tangentiel -qui modifient l'épaisseur de couche limite). En traçant la figure ci-contre il est alors possible de déterminer la propriétés intrinsèque de rétention de la membrane et donc de caractériser sa sélectivité. Ce modèle alors servir à anticiper le taux de rétention que nous devrions observer pour d'autres conditions opératoires. r
Conseil : Il faut toujours comprendre les choses simples avant d'affronter la complexité
Nous verrons dans les niveaux suivants que ce modèle reste cependant un peu simpliste et que le paramètre intrinsèque n'est pas encore vraiment intrinsèque ! Mais un principe important en modélisation puis en programmation est le principe KISS (Keep It Stupidly Simple".
En génie des procédés, on aborde toujours des systèmes complexes (avec des milieux et des mécanismes compliqués en interactions). Il faut alors savoir implémenter la complexité progressivement et garder à l'esprit la phrase attribuée à albert Einstein : “Everything should be as simple as it can be, but not simpler”. Aussi simple que possible (pour favoriser la compréhension) mais pas trop simple (pour décrire la complexité que nous affrontons) !