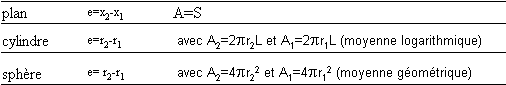Transfert conductif en régime permanent
Considérons le cas le plus simple pour commencer : c'est à dire un transfert thermique par conduction en régime permanent en absence de terme source et en coordonnées rectilignes (nous généraliserons aux autres géométries à la fin de cette partie). Dans ce cas particulier, l'équation de continuité s'écrit : dq/dx=0 Ceci correspond à un flux thermique constant et donc pour un transfert conductif à dT/dx=constante : le profil de concentration de concentration est donc linéaire. |  Expertise |
Vous pourriez mettre en évidence ce type de transfert en réalisant l'expérience suivante. Vous chauffez l'extrémité d'une plaque avec une résistance électrique. Cette résistance va amener un flux de chaleur fixé (en W). Après un régime transitoire (où la température dans la plaque va évoluer), vous allez atteindre une température constante à l'autre bout de la plaque (régime permanent). L'écriture de l'équation de continuité dans la plaque conduit (voir ci-dessus) à déterminer que le profil de température dans la plaque est linéaire. En considérant que la température est respectivement Ti et Te pour les extrémités gauche et droite de la plaque, on peut écrire que :
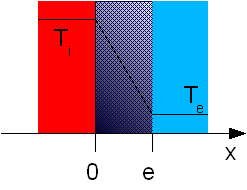
Le flux de matière s'écrit alors :
Pour les données ci-dessus, le flux de matière est donc de .... . Si vous ne disposez pas de capteur de température vous pouvez réaliser cette expérience avec la queue d'une casserole. Si l'eau bout dans la casserole, la température est de 100 °C et vous pouvez disposer sur la queue de la casserole de la cire qui fond à une température de 60 °C. Vous pourrez observer ainsi que plus vous augmentez la puissance du feu plus la cire fond sur des distances par rapport à l'extrémité de la casserole importantes. Mais attention de pas vous brûler !
Il est possible de généraliser les expressions du flux thermique est utilisant la notion de résistance au transfert thermique, Rth. Le produit du flux de chaleur, q, et de la surface pour le transfert S (ce produit correspond au "débit de chaleur" en Joules par secondes ou en Watts) s'écrit :
Cette relation est analogue avec la relation décrivant le transfert d'électron (le courant électrique, I) dans une résistance électrique (R) sous l'effet d'une différence de potentiel (ΔU) : I=ΔU/R. Il s'agit en effet dans le cas du transfert de matière du transfert de matière dans un milieu offrant une résistance sous d'une différence de concentration : la différence de température est le potentiel à transférer la chaleur. De façon générale, la résistance du transfert thermique s'écrit :
où e est l'épaisseur du matériau et A est une surface caractéristique du transfert. On peut démontrer, en résolvant l'équation de continuité pour les différentes géométries, que les valeurs de A et e sont les suivantes : |  Géométries cylindriques et sphériques |